Дерев'яний брус 100х100 мм довжиною 2,5 м горизонтально лежить на бетонному блоці. Ліва частина бруса звисає на 1 м. На ній в 20 см від краю підвішений мотузкою вантаж вагою 6,25 кг. У свою чергу права частина звисає на 75 см. На ній теж мотузка утримує вантаж вагою 20 кг в 25 см від краю. щільність деревини 800 кг / м?. З'ясувати, чи впаде брус при розрізанні мотузки утримує вантаж в 6,25 кг? Що стане з брусом, якщо навпаки, розрізати мотузку, на якій підвішений вантаж в 20 кг?
Для спрощення, приймемо, що прискорення вільного падіння дорівнює 10 м / с ^ 2, тим більше, що воно скорочується. Значить вантажі будуть 62,5 і 200 Н, а питома вага матеріалу бруса 8000 Н / м ^ 3.
1) При розрізуванні мотузки утримує вантаж в 62,5 Н потрібно вважати обертаючі моменти навколо точки дотику брусом правого краю бетонного блоку. Перекидний момент від вантажу 200 Н (плече 0,75-0,25 = 0,5 м) буде дорівнює 200 * 0,5 = 100 Н * м. Момент від звисає частини бруса (0,75 м) компенсується шматочком бруса такої ж довжини (0,75 м), відлічуваним від осі обертання. Нескомпенсованими залишається вага шматочка бруса довжиною 1 м (8000 * 0,1 * 0,1 * 1) = 80 Н, плече цієї ваги складає (1,0 / 2 + 0,75 = 1,25 м). Цей шматок бруса створює утримує момент рівний 80 * 1,25 = 100 Н * м. Моменти рівні, тому система залишиться в рівновазі, тобто. Е. "нічого" не відбудеться.
2) При розрізуванні мотузки, що утримує вантаж 200 Н, потрібно вважати обертаючі моменти навколо точки дотику брусом лівого краю бетонного блоку. Перекидний момент від вантажу 62,5 Н (плече 0,8 м) буде дорівнює 62,5 * 0,8 = 50 Н * м. Момент від звисає частини бруса (1 м) компенсується шматочком бруса такої ж довжини (1 м), відлічуваним від осі обертання. Нескомпенсованими залишається вага шматочка бруса довжиною 0,5 м (8000 * 0,1 * 0,1 * 0,5) = 40 Н, плече цієї ваги складає (1,5-0,25 = 1,25 м). Цей шматок бруса створює утримує момент рівний 40 * 1,25 = 50 Н * м. Моменти рівні, тому система залишиться в рівновазі, тобто. Е. "нічого" не відбудеться.
Хоча завдання і вирішена вірно до мене, але це більше приватно - інтуїтивне рішення. Якби сил і взаємодій було більше, а питання стоїть більш практично, то такий підхід не розкрив би суті завдання. І я не згоден з висновками зробленими в результаті розрахунку.
Ми народжуємося і живемо в світі сил і вміємо в них орієнтуватися. Що таке 10 кг.? Середнє відро води. Це розуміють всі. Гірше справа йде з моментами. Ну ось 50 Н * м, це багато чи мало? Не знаю як Ваша, але моя інтуїція, на цей рахунок, глухо мовчить.
Тому представлю класичний варіант вирішення подібних завдань, де головними "персонажами" будуть сили.
Оскільки при вирішенні такого роду завдань відбувається прирівнювання сил, плечей і моментів, то будь-які розмірності можна скоротити. А відповідь розглядати як безрозмірні коефіцієнти. Тому не будемо торсати дух Ньютона з його прискоренням вільного падіння. Я вибираю сантиметри і кілограми.
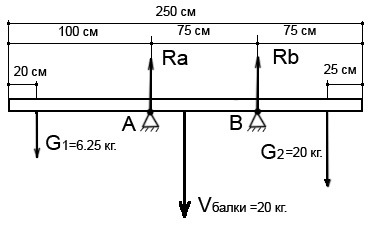
Будь-яке тіло, що знаходиться в стані спокою, взаємодіє з опорою, викликаючи її реакцію. Саме ці сили Ra і Rb врівноважують нашу систему і дають їй спокійненько лежати на камінці.
Якщо при розрахунку реакція опори буде позитивною значить тіло в цій точці тисне на опору, якщо дорівнює нулю, то тільки стикається і якщо негативне значить хоче відірватися від цієї точки. Але яким би не були результати розрахунку, виконається рівність Ra + Rb = G1 + G2 + Vбалкі
Обчислимо масу бруса. Спочатку вираховуємо обсяг в метрах, 1 *, 1 * 2,5 = 0,025 м ^ 3. Далі множимо на щільність 800 кг / м ?. Отримуємо 20 кг. Для спрощення розрахунків, обчислимо свій коефіцієнт 20/250 = 0,08 кг. Це буде вага кожного погонного сантиметра нашого бруса.
Видалимо вантаж G2 = 20 кг
Для того щоб розрахувати реакції опор складемо рівняння моментів, що крутять. Для цього можна вибрати точку А чи В, без різниці. Складемо рівняння щодо точки А при відсутності вантажу G2. Реакція опори Ra в рівнянні не бере, так як її момент відносно точки А дорівнює нулю. Сили позначені червоним кольором, обертають балку за годинниковою стрілкою. Синім кольором - проти.
Обчислюємо вага частин балки знаходяться зліва і право щодо точки А. Знаючи їх довжину і вагу одного погонного сантиметри балки отримуємо: V1 = 8 кг, V2 = 12 кг. Точки прикладання цих сил будуть розташовуватися на середині цих частин балок.
Отримуємо рівняння.
G1 * 80 + V1 * 50 + Rb * 75 = V2 * 12
Звідси Rb = 0, а Ra = 26,25 кг. Тобто точка А прийняла на себе всю вагу системи і вона як би балансує на ній.
Розглянемо систему з відсутністю вантажу G1.
Складаємо рівняння.
V1 * 50 + Rb * 75 = V2 * 75 + G2 * 125
Звідси Rb = 40 кг. і це є всією вагою системи. Значить Ra = 0. Ситуація аналогічна попередній.
В обох випадках, наша система буде знаходиться в стані нестабільної рівноваги. А оскільки ми оперуємо силами, то очевидно, що якщо на балку опуститься хоч одна порошинка, рівновагу буде порушено.
Ви можете заперечити, що про порошинки в умові завдання нічого не сказано. Згоден. Про порошинки не сказано, як і про те що балка є ідеально жорстким тілом. Будь-яке навантаження на балку призводить до її деформації, а зміни схеми розподілу сил, в силу її пружності, змінить її форму. Це в свою чергу викличе переміщення мас балки з подальшим виникненням циклічних сил інерції. Причому величина, частота і коефіцієнт загасання цих сил буде різним у лівої і правої частин балки щодо точки опори. Ці сили безумовно зіграють свою роль в моменті, що крутить системи. Оскільки взаємодія цих сил неможливо передбачити, хоча б в силу неоднорідності матеріалу балки, то в будь-який момент часу вони можуть як зворотно збільшить стабільність системи, так і необоротно її зруйнувати. Що неминуче призведе до падіння залишився вантажу.
Знову ж Ви можете заперечити про малу величину цих сил. Але раз ми вирішуємо завдання теоретично, то 0 + 10 ^ (- 100) це вже не нуль.
Виходячи з умови задачі, мені відповідь представляється наступним.
відповідь
Система знаходиться в стані спокою і падіння, одночасно.
Ось такий котик Шредінгера у мене вийшов.
Та й чому дивуватися. Це абсолютно нормально для системи, де сума моментів дорівнює нулю.
Система знаходиться в рівновазі і буде залишатися в рівновазі якщо акуратно зняти відра, що і показали розрахунки авторів вище. Єдине, що бентежить, так це перерізання мотузки, при якому відбудеться вивільнення сили пружності, яке додасть імпульс і, можливо, його вистачить для подолання сил інерції і деякого повороту балки і вона може заспокоїтися не в горизонтальному положенні, а з нахилом або зовсім перекинутися.
При розрізуванні мотузки утримує вантаж в 6,25 кг перекидаючий момент буде дорівнює 0,5 * 20 = 10 кг * м, а утримує момент під дією маси бруса буде дорівнює 800 * 0,01 * 1,5 = 12 кг * м, тому брус залишиться нерухомим. При розрізуванні мотузки, на якій підвішений вантаж в 20 кг перекидаючий момент буде дорівнює 6,25 * 0,8 = 5 кг * м, а утримує момент буде 800 * 0,01 * 1,75 = 14 кг * м, тому брус теж залишиться нерухомим.
Добавить комментарий