Піфагорійці помилилися в питанні про раціональність музичних інтервалів?
Відповідей: 4
Ставлення частот для октави дорівнює 2, тобто частота «до другої октави» в 2 рази більше частоти «до першої октави». Розподіл октави на 12 рівних півтонів означає, що частота «до дієз» в q разів більше частоти «до», частота «ре» в q разів більше частоти «до дієз», частота «ре дієз» в q разів більше частоти «ре» , частота «ми» в q разів більше частоти «ре дієз», частота «фа» в q разів більше частоти «ми», і т. д., тобто відношення частот для будь-якого півтони дорівнює одному й тому числу q - знаменника геометричній прогресії. Звідси, відношення частот для тону, наприклад, відношення частоти «ре» до частоти «до» дорівнює числу «q в квадраті», ставлення частот для малої терції - «q в кубі», для великої терції «q в четвертого ступеня», для кварти - «q в п'ятого ступеня», для зменшеної квінти - «q ^ 6», для квінти - «q ^ 7», для малої сексти - «q ^ 8», для великої сексти - «q ^ 9», для малої септими - «q ^ 10», для великої септими - «q ^ 11», для октави - «q ^ 12». Прирівнюючи «q в дванадцятому ступені = 2», знаходимо знаменник цієї геометричній прогресії, тобто відношення частот для півтони: q = корінь дванадцятому ступені з 2. Або q = 2 ^ (1/12). Ірраціональність кореня 12 ступеня з числа 2, думаю, можна довести точно також, як і ірраціональність кореня квадратного з числа 2.
Припустимо гидке: 2 ^ (1/12) = m / n, де m і n - цілі числа, а дріб m / n є нескоротного дробом. Тоді m ^ 12 = 2 * n ^ 12. Звідси випливає, що m ^ 12 - парне, отже, число m - теж парне: m = 2 * k.
(2 * k) ^ 12 = 2 * n ^ 12 або 4096 * k ^ 12 = 2 * n ^ 12, скорочуючи на 2 обидві частини рівності, одержимо: 2048 * k ^ 12 = n ^ 12. Отже, число n ^ 12 є парним, отже, і число n є парним, і, так як обидва числа m і n є парними, то це суперечить тому, що дріб m / n є нескоротного дробом.
Так доводиться ірраціональність відносини частот для півтони. Аналогічно, для всіх інших інтервалів крім октави. Усюди виходять ірраціональні числа.
Ставлення частот:
Для малої секунди «до-до дієз»: 2 ^ (1/12) = 1.059463094 ...
Для великої секунди «до-ре»: 2 ^ (2/12) = 2 ^ (1/6) = 1.122462048 ...
Для малої терції «до-мі бемоль»: 2 ^ (3/12) = 2 ^ (1/4) = 1.189207115 ...
Для великої терції «до-ми»: 2 ^ (4/12) = 1 ^ (1/3) = 1.25992105 ...
Для кварти «до фа»: 2 ^ (5/12) = 1.334839854 ...
Для зменшеною квінти «до-сіль бемоль»: 2 ^ (6/12) = 2 ^ (1/2) = 1.414213562 ...
Для квінти «до-сіль»: 2 ^ (7/12) = 1.498307077 ...
Для малої сексти «до-ля бемоль»: 2 ^ (8/12) = 2 ^ (2/3) = 1.587401052 ...
Для великої сексти «до-ля»: 2 ^ (9/12) = 2 ^ (3/4) = 1.681792831 ...
Для малої септими «до-сі бемоль»: 2 ^ (10/12) = 2 ^ (5/6) = 1.781797436 ...
Для великої септими «до-сі»: 2 ^ (11/12) = 1.887748625 ...
Для октави: 2 ^ (12/12) = 2 ^ 1 = 2
Я вважаю, що ваше запитання поставлене не дуже коректно!
Чому піфагорійці помилилися про раціональність музичних інтервалів?
По-перше, вони не помилилися, а так воно і є! Музична гармонія заснована на цілих числах і відносинах. Це так званий 2-й закон Піфагора. Послідовники Піфагора бачили в ЧИСЛІ основу всього. Виявилося, що музичні інтервали підкоряються найпростішим числовим відносинам 2/1 (октава), 3/2 (квінта), 4/3 (кварта)! (Алгебра підтверджує гармонію).
Перевірити 2-й закон Піфагора можна, наприклад, витягуючи флажолети на гітарі. Думаю, за своєю фізіологією вухо людини сприймає як більш гармонійні такі поєднання звуків, які підпорядковані простим числовим відносинам.
По-друге, вживання терміна "раціональність" до "музичним інтервалам" не зовсім коректно. Мабуть, мова йде про те, що в пифагорейском музичному ладі доводилося все таки вводити поправки (пифагорейские Ком), оскільки інакше якщо йти чистими квінтами накопичувалася помилка, що приводить до дисонансу ("вовчої квінті").
Піфагорійський музичний лад по суті став першим музичним ладом. У ньому були використані 12 ступенів. На його основі згодом був побудований натуральний лад. Зміни насамперед торкнулися великої терції, яка, як вважали, звучить дещо натягнуто. Замість співвідношення 81/64 було введено 80/64 (5/4). Але ж для людського вуха 5/4 більш гармонійно, ніж 81/64! Правда, це кілька вибивалося з піфагорейської логіки.
Згодом (в XIX столітті) був введений рівномірно-темперований стрій, який описував співвідношення інтервалів в гамі логарифмическим законом. Один півтон став дорівнює кореню 12-го ступеня з 2. Відмінності від чистих квінти і кварти вийшли досить незначні, на слух практично не помітні.
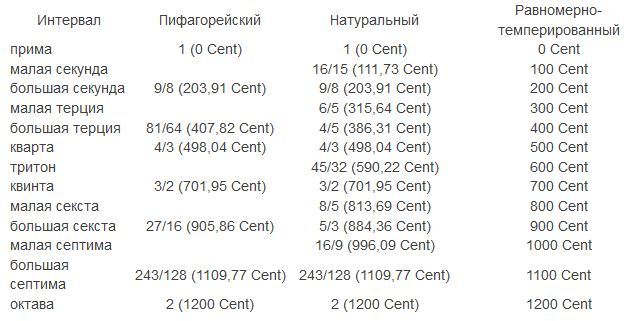
**) У рівномірно-темперований стрій прийнято, що октава = 1200 центів, півтон = 100 центів *.
P.S. Якось я прочитав спогади одного налагоджувальника фортепіано. Він прийшов до парадоксального висновку: коли настроюєш інструмент "неправильним" пифагорейским методом, то як раз в цьому випадку досягається чиста гармонія. Справа в тому що "ідеальних струн" не існує! Велику роль відіграють обертони, що залежать від того, з чого зроблена струна. Обертони впливають на "биття", За якими настроювач судить про точність настройки. А це в теоретичних формули не врахуєш.
Було б дивно, якби Бог, Який створив весь Всесвіт досконалої, сказав:
"З рівномірністю музичного ладу у Мене не вийшло. Ви вже самі як-небудь розберіться з цим!".
Сподіваюся, для Вас це питання так само важливий, як для мене 10 кредитів, хай їм грець. Що власне стосується струн, так, так, звичайно, ось особисто я розумію, чому довжини струн або, як Ви говорите, частоти звукових хвиль серед 12 музичних звуків, що входять в октаву, не можуть ставитися один до одного, як цілі числа, крім октави , звичайно ж, крім неї. А піфагорійці помилилися, але ми з цим вже нічого зробити не зможемо, треба пробачити бідних греків, їм щось останнім часом не щастить. Я ось теж здивувалася, музика це, як Вам сказати, я живу цим ...
Звукові частоти ніби як в герцах міряються. А цілочисельність і герци- це несумісні поняття, так як герци зазвичай зв'язуються з логарифмічним обчисленням, яке, звичайно, не було відомо піфагорійцям.

Добавить комментарий